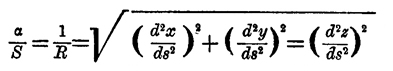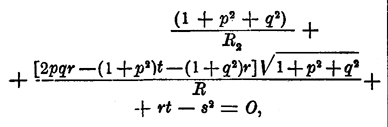Кривизна
Энциклопедия Брокгауза Ф.А. и Ефрона И.А. (1890 - 1916гг.) Статьи для написания рефератов, курсовых работ, научные статьи, биографии (118447 статей и 6000 рисунков).
|
|
| А | Б | В | Г | Д | Е | Ё | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Э | Ю | Я | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | Z |
| К | КЫ | КА | КВ | КГ | КЕ | КЁ | КИ | КЛ | КМ | КН | КО | КР | КС | КТ | КУ | КХ | КШ | КЫ | КЬ | КЭ | КЮ | КЯ |
| КРА |
| КРЕ |
| КРЖ |
| КРИ |
| КРЛ |
| КРО |
| КРС |
| КРУ |
| КРШ |
| КРЫ |
| КРЭ |
| КРЮ |
| КРЯ |
Кривизна — Под большей или меньшей кривизной линии разумеется большее или меньшее уклонение ее от прямолинейного вида, и можно сказать, что окружность тем кривее, чем меньшим радиусом она описана; при очень больших радиусах окружность уклоняется от прямолинейного направления весьма постепенно. Поэтому в математике Кривизна окружности измеряется величиной обратной ее радиусу R; принимают; что Кривизна окружности равна 1/R. Кривизна прочих линий сравнивается с Кривизна окружности следующим образом. К. плоских кривых. Если точка соприкосновения касательной к окружности радиуса R описывает по этой окружности некоторую дугу S, то касательная повертывается при этом на некоторый угол α = S/R. Следовательно, для окружности отношение α /S есть величина постоянная, равная 1/R, то есть Кривизна Отношение α /S угла, составляемого касательными, проведенными в концах дуги S какой-либо кривой, к этой дуге называется средней Кривизна Представим себе, что дуга S кривой уменьшается до совпадения ее концов в одну точку М, тогда отношение α /S стремится к некоторому пределу, который и называется Кривизна в точке М. Окружность, Кривизна которой выражается тем же самым числом как и упомянутый предел, называется кругом К.; радиус ее R — радиусом K. и самая Кривизна кривой в точке М выражается величиной 1/R. Если кривая выражается уравнением f(x,y) = 0, то: 1/R = [d2y/dx2]/[(1 + (dy/dx)2)3/2] = [dx.d2y-dy.d2x]/ds3, где ds = √(dx2+ dy2).
Центр круга Кривизна лежит на нормали точки М и его координаты определяются по формулам X = x — [y'(1 + y'2)]/y" Y = y + (1 + y'2)/y", где y' = dy/dx; y" = d2y/dx2. К. кривых, не умещающихся в плоскости. В кривых таких как винтовая линия, которые описаны в пространстве, первой Кривизна называется тоже предел отношения α /S причем:
Предел положения плоскости, проходящей через точки М и М' кривой и через касательную в точке М, при сближении M' с M назыв. плоскостью соприкосновения. Предел отношения угла, составляемого двумя бесконечно-близкими плоскостями соприкосновения, к соответственной бесконечно малой дуге называется второй К., выражаемой формулой: 1/T = [(d2y.d3z — d2z.d3y)dx + (d2z.d3x — d2x.d3z)dy + (d2x.d3y — d2y.d3x)dz]/[(dy.d2z — dz.d2y)2 + (dz.d2x — dx.d2z)2 + (dx.d2y — dy.d2z)2 ] К. линий, начерченных на поверхности. Эта Кривизна определяется по теореме Менье. Если плоскость соприкосновения в точке M кривой S, начерченной на данной поверхности, составляет угол φ с плоскостью касательной в точке M к поверхности и если R есть радиус Кривизна того нормального сечения, которое имеет с кривой S в точке M общую касательную, то радиус Кривизна кривой S есть R.sin φ. Из всех нормальных сечений, проходящих через какую-либо точку M какой бы то ни было поверхности, существует два, для которых радиус Кривизна достигает максимального или минимального значения — такие два сечения называются главными. Пусть R1 и R2 будут радиусы Кривизна главных сечений, проведенных в точке M поверхности, пусть R есть радиус Кривизна одного из промежуточных сечений и пусть α есть угол, составляемый плоскостью этого промежуточного сечения с сечением соответствующим R1, тогда имеем теорему Эйлера: 1/R = cos2 α /R1 + sin2 α /R2 Если обозначим чрез R' и R" радиусы каких-либо двух перпендикулярных между собой и проходящих через точку М сечений, то: 1/R' + 1/R" = constans. Кривизна 1/R1 и 1/R2 главных сечений суть корни квадр. уравнения:
где p=dz/dx; q=dz/dy; r=d2z/dx2; s=d2z/dx.dy; t=d2z/dy2. Если деформировать (изгибать) нерастяжимую поверхность, то Кривизна начерченных на ней линий изменяется, но Кривизна проекции такой кривой на касательную плоскость для точки соприкосновения остается неизменной. Лиувилль называет эту Кривизна геодезической. Линия, геодезическая Кривизна которой на всем ее протяжении равна нулю, назыв. геодезической; все плоскости соприкосновения геодезической линии нормальны к поверхности. К. поверхностей. Понятие о Кривизна на поверхности было расширено Гауссом следующим образом: начертим на данной поверхности произвольную замкнутую кривую С, ограничивающую некоторую площадь А; проведем из центра сферы, описанной радиусом, равным единице, прямые, параллельные нормалям поверхности, проведенным в точках кривой С. Эти прямые, выходящие из центра сфера, составят конус, который вырежет на сфере некоторую площадь А', которую Гаусс называет интегральной Кривизна При уменьшении площади А до совпадения всех частей ее в одну точку предел отношения A'/A и назван Гауссом К. поверхности в точке М, в которую обратился контур A. Если R1 и R2 радиусы Кривизна главных сечений, то Кривизна поверхности равна 1 /R1R2. Гаусс доказал при этом теорему: интегральная Кривизна треугольника, образованного тремя геодезическими линиями, равна сумме углов этого криволинейного треугольника за вычетом двух прямых. Смотря по тому, имеют ли R1 и R2 одинаковые знаки или противоположные, — Кривизна поверхности будет положительной или отрицательной. Если один из этих радиусов Кривизна R1 или R2 обращается в бесконечность, то Кривизна поверхности равна нулю. Кривизна развертывающихся поверхностей во всех точках равна нулю.
Н. Делоне.
|
Смотрии так же... |
|