Гиперболы
Энциклопедия Брокгауза Ф.А. и Ефрона И.А. (1890 - 1916гг.) Статьи для написания рефератов, курсовых работ, научные статьи, биографии (118447 статей и 6000 рисунков).
|
|
| А | Б | В | Г | Д | Е | Ё | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Э | Ю | Я | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | Z |
| Г | ГА | ГВ | ГД | ГЕ | ГЖ | ГЗ | ГИ | ГЛ | ГМ | ГН | ГО | ГР | ГУ | ГФ | ГХ | ГЫ | ГЬ | ГЭ | ГЮ | ГЯ |
| ГИА |
| ГИБ |
| ГИВ |
| ГИГ |
| ГИД |
| ГИЕ |
| ГИЖ |
| ГИЗ |
| ГИК |
| ГИЛ |
| ГИМ |
| ГИН |
| ГИО |
| ГИП |
| ГИР |
| ГИС |
| ГИТ |
| ГИУ |
| ГИФ |
| ГИХ |
| ГИЦ |
| ГИЧ |
| ГИШ |
| ГИЭ |
| ГИЯ |
Гиперболы — Под этим названием известен в аналитической геометрии ряд кривых линий. 1) Гиперболы второго порядка, или так называемая Аполлониева гипербола. Эта кривая линия была известна уже грекам и принадлежит к числу конических сечений, т. е. получается через сечение прямого кругового конуса плоскостью. В аналитической геометрии гипербола эта, будучи линией второго порядка, определяется уравнением
(1) Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
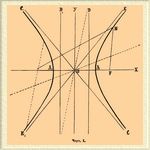
в том случае, когда АС — В 2 < 0, Гиперболы второго порядка состоит из двух отдельных ветвей (черт. 1).
Черт. 1.
Между этими ветвями лежит некоторая точка О, называемая центром Гиперболы, относительно которой точки Гиперболы попарно симметричны; другими словами — всякая прямая, проведенная через центр, пересекает Гиперболы в двух точках, лежащих на одинаковом расстоянии по разные стороны от центра. Из таких секущих, проведенных через центр, существуют две взаимно перпендикулярные ОХ и OY, называемые осями. Относительно этих осей Гиперболы симметрична. Ось ОХ пересекает Гиперболы в двух точках А и А 1, лежащих на разных ветвях Гиперболы и называемых вершинами Гиперболы; другая же ось OY лежит между ветвями Гиперболы и не пересекает ее. Если мы выберем новую систему координат таким образом, что за новое начало координат выберем центр Гиперболы, а за ось х-ов пересекающую ось ОХ Гиперболы, за ось у-ов, не пересекающую ось Гиперболы ОY и уравнение Гиперболы, написанное при старых координатах в виде, приведенном выше, преобразуем по формулам аналитической геометрии для перехода от старых координат к новым, то новое уравнение Гиперболы при новых координатах будет иметь следующий весьма простой вид:
(2) x2 /а 2 — у 2/b2 = 1
где а есть не что иное, как расстояние от центра до одной из вершин и, следовательно, есть так называемая длина действительной полуоси Гиперболы, так, как расстояние от центра до одной из вершин есть половина расстояния между вершинами А и а 1, которое есть не что иное, как длина всей пересекающей оси. Если мы в уравнении (2) во второй части вместо 1 поставим 0, то получим уравнение
(3) x2 /а 2 — у 2/b2 = 0,
определяющее две прямые, проходящие через начало координат, т. е. центр гипербола. В самом деле, уравнение можно переписать так:
(x/a + y/b)(x/a — y/b) = 0,
а оно распадается на два следующих:
x/a + y/b = 0
и
x/a — y/b = 0
определяющих две прямые, называемые асимптотами. Эти асимптоты расположены симметрично относительно осей Гиперболы и наклонены с разных сторон к оси ОХ под углом φ, определяемым из равенства
tang φ = b/a.
Каждая из асимптот пересекает Гиперболы в точке, лежащей на бесконечности. Обе ветви Гиперболы лежат в двух вертикальных углах между асимптотами, при чем они приближаются к асимптотам по мере удаления от центра. Если мы будем пересекать Гиперболы рядом прямых линий, параллельных между собой, то каждая из этих хорд будет иметь две точки пересечения с гиперболой; середины этих параллельных хорд лежат на некоторой прямой, проходящей через центр Гиперболы и называемой диаметром Гиперболы Всякая прямая, проходящая через центр, есть диаметр для хорд некоторого направления. Если теперь мы проведем два диаметра, из которых один параллелен хордам, которые делит пополам другой, то такие два диаметра называются сопряженными. Свойство сопряженных диаметров состоит в том, что каждый из них параллелен хордам, делящимся пополам другим. Две оси суть не что иное, как пара взаимно-перпендикулярных сопряженных диаметров. Если мы один из сопряженных диаметров будем вращать вокруг центра, начиная с положения, совпадающего с осью х-ов, в сторону, обратную движению часовой стрелки, при чем, очевидно, этот диаметр будет приближаться к асимптоте E 1 OE, то сопряженный диаметр будет вращаться в обратную сторону, начиная с положения, совпадающего с осью OY, и стремиться подойти с другой стороны к той же асимптоте Е 1 ОЕ, так что предельным положением такой пары вращающихся сопряженных диаметров будет асимптота Е 1 ОЕ, с которой стремятся совпасть оба диаметра. То же самое будет иметь место по отношению к другой асимптоте С 1 ОС — если мы начнем вращать один из диаметров, начиная с положения ОХ, по направлению часовой строки, приближая к асимптоте С 1 ОС. Уравнения двух сопряженных диаметров имеют вид
l(x/a) + y/b = 0, x/a + l(y/b) = 0;
меняя в этой системе число l, будем получать разные пары сопряженных диаметров: при l = 0 получаются, очевидно, оси; при l = — 1 оба уравнения обращаются в уравнение асимптоты Е 1 ОЕ; при l = 1 получаем асимптоту СОС, при l каком-нибудь, отличном от этих трех чисел, получаем какую-нибудь пару сопряженных диаметров. Остается теперь обратить внимание на две замечательные точки F и F 1, называемые фокусами Гиперболы; эти точки лежат на пересекающей оси Гиперболы в расстоянии от центра, равном √(a2 + b2). Основное свойство этих фокусов состоит в том, что расстояние каждой точки M Гиперболы до одного из этих фокусов выражается линейной функцией от абсциссы точки М. Если эту линейную функцию мы приравняем нулю, то получим уравнение некоторой прямой линии, называемой директрисой. Директрис две: D и D 1; обе они перпендикулярны оси х - ов и лежат по обе стороны оси у-ов на расстоянии, равном a2/√(a2 + b2). Если соединим точку М, лежащую на Гиперболы, с двумя фокусами F и F 1 прямыми MF и МF 1 и обозначим расстояния MF, MF 1 через v и v1, то, если точка М лежит, как это показано на чертеже, на правой ветви Гиперболы, мы получим
v1 — v = 2а;
если же на левой, то
v — v1 = 2a,
другими словами, мы видим, что Гиперболы есть геометрическое место точек, разность расстояний которых от двух заданных, называемых фокусами, есть величина постоянная и равна 2а — длине перестающей оси Гиперболы Из такого определения Гиперболы следует весьма простой механический способ черчения этой кривой. Если возьмем полярные координаты, причем полюс поместим в одном из фокусов Гиперболы, а полярную ось направим по пересекающей оси Гиперболы, тогда уравнение Гиперболы принимает следующий замечательный вид, употребляемый в астрономии:
r = p/(1 + eCos Θ),
где r и Θ суть полярные координаты точки на Гиперболы: r — расстояние точки до полюса, так называемый радиус вектор точки, а Θ — угол, составляемый радиусом вектором с полярной осью; p есть так называемый параметр Гиперболы и равняется b2/a, т. е. ординате у, соответствующей фокусу;
е = √(a 2 + b2)/a
называется астрономическим эксцентриситетом гиперболы; число е больше единицы и показывает, во сколько раз расстояние фокуса до центра больше расстояния вершины до центра. Дадим теперь геометрическое толкование числу b. Если мы в уравнении (2) во второй части переменим + 1 на — 1, т. е. возьмем
x2 /а 2 — у 2/b2 = — 1,
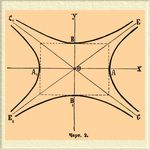
то получим новую Гиперболы, называемую сопряженной, при чем эта новая Гиперболы займет другую пару вертикальных углов между асимптотами, как показано на чертеже. Для сопряженной Гиперболы центр и асимптоты будут те же, что и для заданной. Перестающая же ось для сопряженной Гиперболы совпадает с мнимой осью первоначальной, при чем длина этой оси BB 1 будет, очевидно, равна 2b. Укажем теперь на свойства сопряженных диаметров, замеченные Аполлонием. Так как сопряженные диаметры лежат в разных вертикальных углах, образуемых асимптотами, то очевидно, что один из них пересекает в двух точках заданную Гиперболы, а другой — сопряженную. Назовем длину полудиаметра, пересекающего заданную Гиперболы, через а 1, а длину сопряженного полудиаметра, пересекающего Гиперболы сопряженную, через b1, тогда будет иметь место для всякой пары сопряженных диаметров равенство
a12 —b12 = a2 —b2,
т. е. разность квадратов сопряженных полудиаметров в Гиперболы есть величина постоянная, равная разности квадратов полуосей. В четырех точках пересечения заданной Гиперболы и сопряженной двумя сопряженными диаметрами проведем четыре касательные линии; эти касательные образуют параллелограмм, вершины которого лежат на асимптотах, стороны же, очевидно, параллельны рассматриваемым диаметрам. Площадь этого параллелограмма есть величина постоянная, равная 4аb, т. е. площади прямоугольника, построенного на осях.
Черт. 2.
Если числа а и b равны между собой, то уравнение Гиперболы будет иметь вид
х 2 — у 2 = а 2,
причем Гиперболы будет так называемая равносторонняя, ее асимптоты будут взаимно перпендикулярны, а сопряженная Гиперболы будет подобна заданной, при чем поворотом на 90° вокруг центра может быть совмещена с заданной. Равносторонняя Гиперболы играет ту же роль относительно разносторонней, какую круг относительно эллипса. Если мы возьмем асимптоты за координатные оси, тогда уравнение Гиперболы примет вид
xy = k2,
где k — число постоянное, зависящее от полуосей.
2) Змеевидная Гиперболы — так наз. линия, определяемая уравнением
xy2 + aby — a2 х = 0.
3) Гиперболы высшего порядка — так наз. линии, определяемые уравнением
xnym = a,
где m и n числа целые, положительные. При n = m = 1 последнее уравнение даёт Гиперболы второго порядка. Асимптотами этих Гиперболы служат оси координат.
Д. Граве.
|
Смотрии так же... |
|