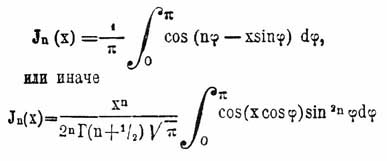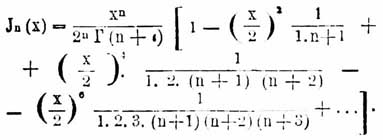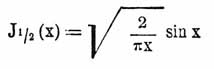Бесселевы функции
Энциклопедия Брокгауза Ф.А. и Ефрона И.А. (1890 - 1916гг.) Статьи для написания рефератов, курсовых работ, научные статьи, биографии (118447 статей и 6000 рисунков).
|
|
| А | Б | В | Г | Д | Е | Ё | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Э | Ю | Я | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | Z |
| Б | БА | ББ | БГ | БД | БЕ | БЁ | БЖ | БЗ | БИ | БЛ | БМ | БН | БО | БР | БУ | БХ | БЫ | БЬ | БЭ | БЮ | БЯ |
| БЕА |
| БЕБ |
| БЕВ |
| БЕГ |
| БЕД |
| БЕЕ |
| БЕЖ |
| БЕЗ |
| БЕЙ |
| БЕК |
| БЕЛ |
| БЕМ |
| БЕН |
| БЕО |
| БЕР |
| БЕС |
| БЕТ |
| БЕУ |
| БЕФ |
| БЕХ |
| БЕЦ |
| БЕЧ |
| БЕШ |
| БЕЯ |
Бесселевы функции или цилиндрические функции, или цилиндрические гармоники — выражения, введенные в анализ и в особенности в небесную механику немецким астрономом Бесселем и потому носящие его имя. Во Франции еще раньше Бесселя подобные функции рассматривал Фурье в теории теплоты, и потому их называют также иногда еще функциями Фурье-Бесселя. Бесселевы функции ф. можно ввести в рассмотрение весьма различным образом, смотря по той цели, к которой они применяются. Можно исходить из некоторых разложений в ряд тригонометрический, или по степеням независимой переменной, или из дифференциального уравнения второго порядка, которому удовлетворяют эти функции. Обозначая функции 0-го, 1-го, 2-го... порядка, как это общепринято, буквами J 0(x), J1(x), J2 (x)... имеем, например:
cos(xsin φ) = J0(x) + 2J2(x)cos2 φ + 2J4(x)cos4 φ + …
sin(xsin φ) = 2J1(x)sin φ + 2J3(x)sin3 φ + …
или e ½x(z—1/z) = J0(x)+J2(x)[z2+(1/z2)]+J0(x)[z4+(1/z4)]+J1(x)(z — 1/z)+J3(x)(z3 — 1/z3)+…,
а дифференциальное уравнение, которому удовлетворяют Бесселевы функции функции n-го порядка, есть
d2Jn(x)/dx2 + (1/x)(dJn(x)/dx + [1 — n2/x2]Jn(x) = 0
Между тремя последовательными Б-ми функциями существует простое соотношение:
xJn + 1(x) — 2nJn(x) + xJn — 1(x) = 0
из которого явствует, что достаточно знать значения двух каких-нибудь из Бесселевы функции-вых функций, напр. J 0 и J 1, чтобы можно было найти все остальные посредством простых арифметических операций. Отсюда же легко получить следующую непрерывную дробь, позволяющую вычислять с произвольной степенью точности значения какой угодно Б-вой функции:
P = (½n)/x — [1/(2n+2)]/x — [1/(2n+4)]/x — …
Для этого стоит только положить J n = pnJn — 1, откуда будет вообще Jn = p 1 p2 ... pn J0, а это непосредственно приводит к написанной непрерывной дроби. Бесселевы функции-вы функции могут также быть представлены и притом несколькими способами в виде определенного интеграла, а именно:
Разложенная в ряд Б-ва функция n-го порядка есть:
Определение Бесселевы функции-вой функции посредством определенного интеграла или ряда может быть распространено и на случай нецелого значения показателя n с условием в последнем случае n + 1 больше 0. Так, напр., из интеграла получается:
Употребление функций Бесселя в анализе, в теории теплоты и в небесной механике основано на том, что многие разложения в ряд могут быть сделаны с удобством посредством именно этих функций. Так, напр., имеем:
cosx = J0(x) — 2J2(x) + 2J4(x) — …
sinx = 2J1(x) — 2J3(x) + 2J5(x) — …
½ = 1/2J0(x) + J2(x) + J4(x) + …
½x = J1(x) + 3J3(x) + 5J5(x) + …
½x2 = 22J2 (х) + 4 2J4 (х) + …
½x3= 3(32 — 1)J3(x) + 5(52 — 1)J5(x) + …
Такие разложения в ряд играют важную роль в теории возмущений планетных движений. Эти же функции интегрируют в анализе известное дифференциальное уравнение Риккати. Заметим в заключение, что функции Бесселя можно рассмативать как частный случай функций Лежандра, или шаровых функций, или сферических гармоник, т. е. функций, удовлетворяющих уравнению:
(1 — x2)d2Pm/dx2 — (2x)dPm/dx + m(m + 1)Pm = 0
для случая m = ∞, а именно вводя новую переменную ξ и новую функцию η положениями
ξ = m√(1—x2)
η = (1 — x2)½n(dnPn/dxn)
получим, полагая m бесконечно большим, дифференциальное уравнение, удовлетворяемое Бесселевы функции-ою функцией n-го порядка, написанное выше.
Литература. Работы самого Бесселя о функциях, носящих его имя, помещены в собрании его сочинений, изд. Энгельмана т. I. Затем специально Бесселевы функции-м функциям посвящены труды: Неймана (Neumann), "Theorie der Bessel'schen Functionen"; Ломмеля (Lommel), "Studien ü ber die Bessel'schen Functionen". Весьма полное исследование этих функций можно найти в трактате Гейне (Heine) "Handbuch der Kugelfunctionen" (2-е изд.) и в более элементарном учебнике Тодгентера (Todhunter), "An elementary Treatise on the functions of Laplace, Lam é and Bessel". Таблицы численных значений Бесселевы функции-вых функций для практических приложений их находятся в работе Бесселя, в статье Гансена об определении абсолютных возмущений и подробнее других в специальных таблицах Мейсселя (Meissel).
|
Смотрии так же... |
|