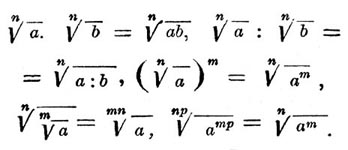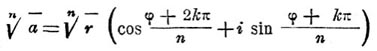Радикал, в математике
Энциклопедия Брокгауза Ф.А. и Ефрона И.А. (1890 - 1916гг.) Статьи для написания рефератов, курсовых работ, научные статьи, биографии (118447 статей и 6000 рисунков).
|
|
| А | Б | В | Г | Д | Е | Ё | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Э | Ю | Я | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | Z |
| Р | РА | РБ | РВ | РГ | РД | РЕ | РЖ | РИ | РК | РО | РТ | РУ | РШ | РЫ | РЭ | РЮ | РЯ |
| РАА |
| РАБ |
| РАВ |
| РАГ |
| РАД |
| РАЕ |
| РАЖ |
| РАЗ |
| РАИ |
| РАЙ |
| РАК |
| РАЛ |
| РАМ |
| РАН |
| РАО |
| РАП |
| РАР |
| РАС |
| РАТ |
| РАУ |
| РАФ |
| РАХ |
| РАЦ |
| РАЧ |
| РАШ |
| РАЯ |
Радикал, в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается 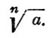 Здесь а называется подкоренным числом, n — показателем корня. Радикал называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Радикал подразумевается число положительное. Алгебраическое выражение, содержащее Радикал, может подвергаться преобразованиям при помощи формул:
Здесь а называется подкоренным числом, n — показателем корня. Радикал называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Радикал подразумевается число положительное. Алгебраическое выражение, содержащее Радикал, может подвергаться преобразованиям при помощи формул:
Если данное выражение имеет вид дроби, знаменатель которой содержит Р., то, помножая числитель и знаменатель на выражение, надлежащим образом подобранное, можно удалить все Радикал из знаменателя. При помощи средств начальной алгебры можно выполнить это преобразование только в простейших случаях. В высшей алгебре подкоренное число a предполагается комплексным (см. Мнимые величины) и представляется под видом
a = r(cos φ + isin φ), где r > 0.
Для n значений Радикал получается выражение
где k = 0, 1, 2,..., n— 1. В правой части 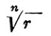 положительное число, n -ая степень которого равна r. При помощи Радикал можно выразить корни каких угодно уравнений второй, третьей и четвертой степени. Решать же уравнения высших степеней при помощи Радикал возможно только в исключительных случаях, как это выяснилось благодаря исследованиям Абеля и Галуа. В соч. Д. Селиванова "Об уравнениях пятой степени с целыми коэффициентами" (СПб. 1889) приведены примеры уравнений, нерешаемых алгебраически. Оказывается, что напр. уравнение х5— х —v = 0 не решается в Радикал, если v не делится на 15. Если в алгебраическом решении уравнения все показатели Радикал равны двум, то корни можно построить при помощи циркуля и линейки. На этом основании Гаусс в своем сочинении "Disquisitiones arithmeticae" (в "Ganss Werke", т. I) указал, какие правильные многоугольники можно вписать в круг при помощи циркуля и линейки. К числу таких многоугольников принадлежит семнадцатиугольник.
положительное число, n -ая степень которого равна r. При помощи Радикал можно выразить корни каких угодно уравнений второй, третьей и четвертой степени. Решать же уравнения высших степеней при помощи Радикал возможно только в исключительных случаях, как это выяснилось благодаря исследованиям Абеля и Галуа. В соч. Д. Селиванова "Об уравнениях пятой степени с целыми коэффициентами" (СПб. 1889) приведены примеры уравнений, нерешаемых алгебраически. Оказывается, что напр. уравнение х5— х —v = 0 не решается в Радикал, если v не делится на 15. Если в алгебраическом решении уравнения все показатели Радикал равны двум, то корни можно построить при помощи циркуля и линейки. На этом основании Гаусс в своем сочинении "Disquisitiones arithmeticae" (в "Ganss Werke", т. I) указал, какие правильные многоугольники можно вписать в круг при помощи циркуля и линейки. К числу таких многоугольников принадлежит семнадцатиугольник.
Д. Селиванов.
|
Смотрии так же... |
|