Анализ математический
Энциклопедия Брокгауза Ф.А. и Ефрона И.А. (1890 - 1916гг.) Статьи для написания рефератов, курсовых работ, научные статьи, биографии (118447 статей и 6000 рисунков).
|
|
| А | Б | В | Г | Д | Е | Ё | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Э | Ю | Я | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | Z |
| А | АА | АБ | АВ | АГ | АД | АЕ | АЖ | АЗ | АИ | АЙ | АК | АЛ | АМ | АН | АО | АП | АР | АС | АТ | АУ | АФ | АХ | АЦ | АЧ | АШ | АЩ | АЭ | АЮ | АЯ |
| АНА |
| АНВ |
| АНГ |
| АНД |
| АНЕ |
| АНЖ |
| АНЗ |
| АНИ |
| АНК |
| АНН |
| АНО |
| АНР |
| АНС |
| АНТ |
| АНУ |
| АНФ |
| АНХ |
| АНЦ |
| АНЧ |
| АНШ |
| АНЬ |
| АНЭ |
| АНЮ |
Анализматематический как самостоятельная система есть алгебра в обширном смысле этого слова, которая рассматривает все величины как неизвестные числа, употребляя буквы вместо арифметических знаков-цифр. Включая в математический Анализ математический учение о равенствах, составляющее предмет низшей алгебры, можно последнюю рассматривать как первую часть Анализ математический, коего вторая часть, собственно Анализ математический, занимается исследованием конечных и бесконечных величин. Анализ математический конечных величин, называемый также "Теорией функций", есть учение о формах величин и обнимает теории рядов, соединений, логарифмов, в то время как Анализ математический бесконечных величин, излагаемый обыкновенно под названием высшего Анализ математический, состоит из трех главных частей: дифференциального, интегрального и вариационного исчислений. Основателями этих учений принимают обыкновенно Ньютона и Лейбница, но, собственно говоря, Эйлер впервые в своем "Introducti o in analysim infinitorum" (1748) придал Анализ математический систематическую форму. Анализ математический древних математиков отличался от нового, современного нам Анализ математический тем, что у древних Анализ математический относился только к геометрии и состоял в применении аналитического метода к решению геометрических задач, причем искомое предполагалось найденным, исследовалось и после ряда логических рассуждений получалось либо подтверждение известного положения, либо отрицание его возможности. Обратный способ действий характеризует синтетический метод, т. е. метод определения искомого путем определенного строения. Открытие геометрического Анализ математический приписывают почему-то Платону, хотя от него не дошло до нас никаких математических трактатов. В начале XVII столетия наступила цветущая эпоха для Анализ математический вообще и геометрического в частности; по примеру Ньютона Анализ математический начинают особенно заниматься английские математики, которые и возвели здание так наз. бесконечного Анализ математический
Чтобы сравнить Анализ математический с синтезом, прибавим, что в первом методе разлагают исследуемую истину на части, которые должны быть верны и между собою связаны, если данная задача верна, или эти составные части окажутся неверными и не связанными между собою, если задача математически неверна; при втором же методе на основании как-нибудь связанных между собою нескольких истин выводят новые, их объединяющие. Выражаясь фигурально, в Анализ математический идут от вершины к корню, а в синтезе — в обратном порядке. Поясним этот процесс примерами:
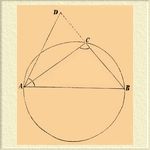
Задача I. Найти на сегменте данного круга ВСА такую точку С, чтобы проведенные от нее прямые СА и СВ до концов хорды AB находились в отношении M к N?
Анализ. Предположим, что искомая точка С найдена; проведя прямые СА и СВ, получим AC: BC = M: N (см. фиг. I).
Фиг. I.
Если мы проведем еще прямую AD так, чтобы угол BAD равнялся углу АСВ, и продолжим ВС до D, то получим два треугольника АСВ и BAD с равными углами и, следовательно, подобные; отсюда составим пропорцию AC: BC: AD: AB; очевидно, AD: AB = M: N. В последней пропорции AB величина известная, а AD вполне определенная; на основании их можно дойти легко до решения данной задачи.
Синтез. Проводим из точки А прямую AD, которая с данной хордой AB даст угол BAD, равный тому углу, который может дать сегмент ВСАнализ математический Эта прямая должна быть четвертой пропорциональной прямым AB, M и N; находим прямую BD, которая пересечет окружность в искомой точке С. Для доказательства подобного построения поясним, что треугольники ABC и ABD подобны, так как угол В общий, а угол BAD по построению равен всем углам, которые может дать сегмент, следовательно, и углу ВСАнализ математический Из подобия треугольников выводим, что АС: BC = AD: АВ = M: N; таким образом, АС и ВС окажутся между собою в искомом отношении.
Задача II. В данный треугольник вписать квадрат?
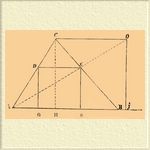
Анализ. Пусть ABC данный треугольник (см. фигуру II).
Фиг. II.
Предположим задачу решенною: DESG — вписанный квадрат. Проведем через точки А и E прямую АЕ до встречи в точке О с линиею СО, параллельною AB. Продолжим далее AB и опустим на нее перпендикуляр OJ из точки O; равным образом опустим из вершины С треугольника перпендикуляр СН, который будет высотою данного треугольника. Ясно, что треугольники АСО в ADE подобны, так же как и треугольники AOJ и AEF. Из подобия их выводим следующие пропорции: AE: AO = DE : CO и АЕ: АО; EF: OJ. B обеих пропорциях первые три члена равны, так как DE = EF, как стороны квадрата; следовательно, и СО равно OJ, или CO = OJ = CH. Итак, четырехугольник COJH будет квадратом, стороны которого равны высоте данного треугольника. Отсюда и определяется положение точки Е, на основании которой и решается задача.
Синтез. На высоте СH данного треугольника строим квадрат CHJO; соединяем точки А и О прямой АО. Из точки Е пересечения прямой АО и стороны треугольника СВ опускаем перпендикуляр EF на сторону AB и проводим ED, параллельную линии AB. Опустив из найденной точки D перпендикуляр DG, получаем искомый вписанный квадрат DEFG. Для доказательства подобного построения замечаем, что треугольники AED и AOC подобны, равно как и AEF и AOJ. Поэтому АО: АЕ = СО: DE и AO: AE = OJ: EF; но CO = OJ по построению; следовательно, DE и EF равны, а потому DE = EF = FG = DG, т. е. фигура DEFG имеет все стороны равными и есть квадрат, вписанный в треугольник, что и требовалось построить.
Приведенных двух примеров достаточно для выяснения разницы методов анализа и синтеза в применении к математике.
|
Смотрии так же... |
|