Эллипсоид*
Энциклопедия Брокгауза Ф.А. и Ефрона И.А. (1890 - 1916гг.) Статьи для написания рефератов, курсовых работ, научные статьи, биографии (118447 статей и 6000 рисунков).
|
|
| А | Б | В | Г | Д | Е | Ё | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Э | Ю | Я | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | Z |
| Э | ЭА | ЭБ | ЭВ | ЭГ | ЭД | ЭЕ | ЭЖ | ЭЗ | ЭЙ | ЭК | ЭЛ | ЭМ | ЭН | ЭО | ЭП | ЭР | ЭС | ЭТ | ЭУ | ЭФ | ЭХ | ЭЦ | ЭЧ | ЭШ | ЭЭ | ЭЮ | ЭЯ |
| ЭЛА |
| ЭЛЕ |
| ЭЛИ |
| ЭЛК |
| ЭЛЛ |
| ЭЛМ |
| ЭЛО |
| ЭЛУ |
| ЭЛЬ |
| ЭЛЮ |
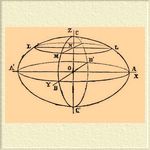
Эллипсоид* — Поверхность второго порядка, замкнутая, имеющая центр и пересекаемая всякой плоскостью по эллипсам или кругам, называется Эллипсоид* На прилагаемом чертеже изображен Эллипсоид* с тремя неравными главными взаимно перпендикулярными полуосями: большой а = OA, средней b = OB и малой с = ОС. Если начало координата взято в центре О Эллипсоид*, ось X-ов расположена по A'ОА, ось Y -ов по B'ОВ и ось Z -ов по C'OC, то уравнение Эллипсоид* будет:
x2/a2 + y2/b2 + z2/c2 = 1. (1)
Поверхность эта обладает, между прочим, следующими геометрическими свойствами. Если через какую-нибудь точку её провести касательную к ней плоскость, то пересечения всех плоскостей, ей параллельных, с поверхностью Эллипсоид* будут эллипсы, подобные друг другу, с параллельными между собой большими главными осями и с параллельными между собой главными малыми осями.
Та плоскость, параллельная касательной плоскости, которая проходит через центр Эллипсоид*, называется диаметральной плоскостью, сопряженной диаметру, проведенному через центр и точку касания. Диаметры А'А, B'B, C'С называются главными диаметральными, а плоскости эллипсов CВC'В ', ACA'C', ABA'B' — главными диаметральными плоскостями. На главном диаметральном эллипсе АСА'C' имеются четыре точки, расположенные на концах двух диаметров этого эллипса, наклоненных к оси Х-ов под углами, тангенсы которых равны
+ (с/a)√ [(b2—c2 )/(a2—b2)], — (с/a)√ [(b2—c2 )/(a2—b2)].
Точки эти называются точками закругления. Касательные плоскости к Эллипсоид*, проведенные в этих точках, параллельны оси Y -ов и, значит, перпендикулярны в плоскости XOZ. Плоскости, секущие Эллипсоид* и параллельные этим плоскостям, дают не эллиптические, но круговые сечения. Те две проходящие через центр плоскости, которые сопряженны двум диаметрам точек закругления, пересекают Эллипсоид* по двум кругам радиуса b, проходящим через ось Y -ов.
Эллипсоид* инерции, вращение твердого тела вокруг неподвижной точки по uнepцuu.
В статье: Момент инерции (см.) было объяснено значение Эллипсоид* инерции твердого тела для какой-либо точки и значение главных осей инерции.
Если А = ∑ m(y2 + z2), В = ∑m(z2 + x2), С = ∑ m(x2 + у 2) суть моменты инерции вокруг главных осей инерции, проведенных через рассматриваемую точку тела, то величины главных полуосей Эллипсоид* инерции обратно пропорциональны корням квадратным из этих главных моментов инерции, т. е. a = (√A) —1, b = (√B)—1, c = (√C) —1, тогда уравнение Эллипсоид* инерции принимает вид (1). Надо, однако, заметить, что не всякий Эллипсоид* может быть Эллипсоид* инерции; надо, чтобы величины полуосей а, b, с удовлетворяли некоторому условию. Можно убедиться, что: A + B — C = 2∑mz2 и, следовательно, эта величина всегда положительная; поэтому a2, b2 и с2 должны удовлетворять условию:
(a2) —1 + (b2 ) —1 — (c2) —1 > 0.
Например, Эллипсоид*, полуоси которого суть а = 3, b = 2, с = 1 не может быть Эллипсоид* инерции никакого тела, потому что 1/9 + 1/4 + —1<0.
В тех случаях, в которых Эллипсоид* инерции есть Эллипсоид* вращения, то есть когда b = a, то предыдущее условие обратится в следующее:
2/a2 > 1/с2,
откуда с должно быть больше a/√2. Следовательно, Эллипсоид* инерции может быть удлиненным Эллипсоид* вращения при произвольной длине с, большей экваториальной полуоси а, но сжатый или планетарный Эллипсоид* может быть Эллипсоид* инерции, если малая полуось с не меньше экваториальной полуоси а, деленной на √2. Если твердому телу, имеющему неподвижную точку, сообщить какой-либо толчок, приводящий его во вращение вокруг этой точки, и если на тело не действуют никакие внешние силы, то вращение, совершаемое телом, называют вращением по инерции. При таком вращении живая сила вращательных движений всего тела остается постоянной; остается также постоянным и момент количества движения всего тела вокруг неподвижной точки (см.). Момент количества движений всего тела (так назыв. главный момент количества движений тела) может быть изображен линейно, в виде вектора (см.), т. е. длины, проведенной из неподвижной точки. Длина эта остается при вращении по инерции постоянной, и направление её остается в пространстве неизменным. Пуансо (см.) показал, что геометрический характер вращения твердого тела по инерции может быть выражен следующим образом. Тот Эллипсоид* инерции твердого тела, центром которого служит неподвижная точка, катится без скольжения по двум плоскостям, перпендикулярным к главному моменту количества движения и находящимся на равных постоянных расстояниях по обе стороны неподвижной точки. При катании без скольжения мгновенная ось вращения (см.) проходит через точки прикосновения Эллипсоид* к неподвижным плоскостям. Та кривая линия, которую описывает каждая из двух этих точек прикосновения на поверхности Эллипсоид*, называется noлoдиeю, a та кривая, которую эта точка описывает на неподвижной плоскости, называется эрполодиею. Величина расстояния выше сказанных плоскостей от неподвижной точки зависит от величины живой силы вращения твердого тела и от величины главного момента количества движения. Расстояния эти ни в каком случае не могут быть больше большой полуоси и меньше малой полуоси Эллипсоид* инерции. Если расстояния эти равны большой, средней или малой полуоси этого Эллипсоид*, то полодии и эрполодии обращаются в точки. Тогда вращение по инерции твердого тела будет совершаться равномерно вокруг одной из главных осей Эллипсоид* инерции, и самая ось будет сохранять неизменное направление в пространстве. По этой причине главные оси Эллипсоид* инерции называются главными осями инерции. Когда Эллипсоид* инерции есть Эллипсоид* вращения, то полодии суть параллельные круги на Эллипсоид* и эрполодии суть круги на неподвижных плоскостях. Вращение по инерции такого тела состоит из вращения вокруг оси симметрии Эллипсоид*, причем эта ось равномерно описывает прямой конус вокруг главного момента количества движения. Вращение это аналогично тому, которое описано в конце статьи Вращательное движение (см.).
Эллипсоид* упругости и Эллипсоид* деформаций. Ламе (см.) ввел в теорию упругости представление об Эллипсоид* упругости. Напряжения сил упругости (см. Упругость), действующие на площадки, проходящие через одну и ту же точку упругого тела, имеют различные величины и направления в зависимости от направления нормали. Если изобразить напряжения, приложенные к площадкам всевозможных направлений (но проходящих через одну и ту же точку), длинами, отложенными по направлениям напряжений, то оконечности этих длин образуют поверхность Эллипсоид* упругости. Ничтожно малые деформации, совершающиеся при переходе упругого тела из естественного состояния в деформированное, происходят так, что если вокруг какой-нибудь точки опишем шар весьма малого радиуса, то частицы, находившиеся в естественном состоянии внутри и на поверхности этого шара, в деформированном состоянии будут находиться внутри и на поверхности некоторого Эллипсоид* Обратно, можно вокруг точки как вокруг центра описать такой Эллипсоид*, который при деформации обратится в шар; Эллипсоид* этот называется Эллипсоид* деформации.
Д. Б.
|
Смотрии так же... |
|