|
Иллюстрация к статье на тему "Монмор Пьер де". Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
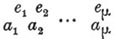
Монмор Пьер де - — французский математик (1678—1719). Настоящая его фамилия Ремон (R é mond de Montmort), Монмор Пьер де же называлось особенно любимое им поместье. В юности Монмор Пьер де изучал правоведение и философию, но его влекло к математике, которую он после путешествия по Германии и сделал почти исключительным предметом своих занятий. Монмор Пьер де поддерживал постоянные сношения с Николаем И. Бернулли и многими другими математиками, французскими и иностранными (Мальбранш, Моавр, Франсуа Николь, Иоанн Бернулли, Тайлор и Конти). Монмор Пьер де переписывался также и с Лейбницем, мнение которого о Монмор Пьер де как математике вообще было так высоко, что он выбрал его в 1716 году посредником в своем споре с Ньютоном о первенстве открытия анализа бесконечно малых. Ученые труды Монмор Пьер де относились главным образом к теории вероятностей и к учению о рядах. В последние годы своей жизни Монмор Пьер де занимался составлением "Истории геометрии", которая, по-видимому, не была окончена. Его исследования по теории вероятностей изложены в особом составленном им сочинении, вышедшем в свет в 1708 г. под заглавием "Essay d'Analyse sur les jeux de Hazard", но без имени автора. В своем значительно пополненном и улучшенном втором издании, в 1713 году, это сочинение состояло из 5 отделений, из которых первое было посвящено необходимому для последующего изложения учению о соединениях вместе с относящимися к нему исследованиями самого автора; второе, третье и четвертое занимались главным предметом всего сочинения, то есть играми, вероятности выигрыша в которых исследовались с помощью учения о соединениях, и, наконец, пятое содержало относящуюся к предмету сочинения, по крайней мере в главной своей части, переписку автора с Иоанном и Николаем И. Бернулли. Монмор Пьер де первый обращает здесь внимание на отношения, существующие между числами вероятностей и полиномиальными коэффициентами. Также здесь говорит он, что если включить 1 в число делителей и подразумевать под а1, а2,... 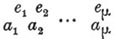а μ простые числа, то число делителей выражения  представится произведением (e1+1) (e2+1)... ( е μ + 1). Наконец, он составляет фигурные числа из вновь появляющихся с каждой новой строкой производящих чисел, которые называются им generateurs. Работы Монмор Пьер де в области учения о рядах относились главным образом к суммированию последних и послужили предметом нескольких мемуаров, представленных автором в Лондонское королевское общество и затем напечатанных в "Philosophical Transactions". В одном, из этих мемуаров, появившемся в свете в 1717 г. ("Ph. Tr." XXX, стр. 633—675), автор занимается развитием и приложением к разнообразным примерам идеи о том, что при суммировании ряда все усилия должны быть направлены к представлению его членов в виде таких разностей, в которых вычитаемое одной служило бы уменьшаемым для непосредственно следующей за ней другой. Сумма рассматриваемого ряда при таком выражении очевидна. В другом мемуаре (1718 г.) Монмор Пьер де первый дал и доказал замечательную формулу, служащую для выражения суммы p членов ряда, разности которых доходят до обращения в нуль. Если обозначить через а член, с которого начинается суммирование, а через Δ а, Δ 2а, ... разности различных порядков, доставляемые следующими членами, то эта формула представится в виде
|
представится произведением (e1+1) (e2+1)... ( е μ + 1). Наконец, он составляет фигурные числа из вновь появляющихся с каждой новой строкой производящих чисел, которые называются им generateurs. Работы Монмор Пьер де в области учения о рядах относились главным образом к суммированию последних и послужили предметом нескольких мемуаров, представленных автором в Лондонское королевское общество и затем напечатанных в "Philosophical Transactions". В одном, из этих мемуаров, появившемся в свете в 1717 г. ("Ph. Tr." XXX, стр. 633—675), автор занимается развитием и приложением к разнообразным примерам идеи о том, что при суммировании ряда все усилия должны быть направлены к представлению его членов в виде таких разностей, в которых вычитаемое одной служило бы уменьшаемым для непосредственно следующей за ней другой. Сумма рассматриваемого ряда при таком выражении очевидна. В другом мемуаре (1718 г.) Монмор Пьер де первый дал и доказал замечательную формулу, служащую для выражения суммы p членов ряда, разности которых доходят до обращения в нуль. Если обозначить через а член, с которого начинается суммирование, а через Δ а, Δ 2а, ... разности различных порядков, доставляемые следующими членами, то эта формула представится в виде