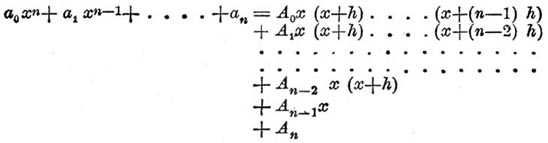|
Иллюстрация к статье на тему "Исчисление конечных разностей". Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
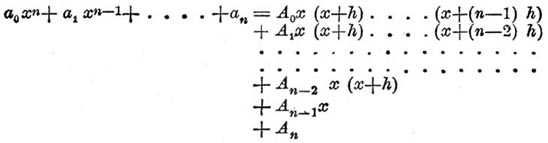
Исчисление конечных разностей - — Конечной разностью функции от одной или нескольких переменных называется приращение функции при данных конечных приращениях переменных независимых. Под Исчисление конечных разностей конечных разностей разумеют совокупность правил: 1) для определения изменений, которым подвергаются функции при конечных приращениях входящих в них переменных, и 2) для определения первообразных функций, когда измененные их виды известны (прямой и обратный способы). При первом появлении дифференциального исчисления приращения переменных величин рассматривались как бесконечно малые величины, вторыми и высшими степенями которых пренебрегали, вследствие чего у многих из математиков явилось сомнение в строгости самого способа и верности результатов, получаемых дифференциальным исчислением. Чтобы доказать справедливость нового способа, английский математик Тейлор, в своем сочинении " Methodus incrementorum directa et inversa", изданном в 1715 году, предложил способ Исчисление конечных разностей конечных разностей, в котором приращения переменных рассматривались как конечные величины, высшими степенями которых уже нельзя пренебрегать. Однако Исчисление конечных разностей конечных разностей, представляющее в сущности Исчисление конечных разностей рядов, имеет, как заметил Лагранж, мало общего с дифференциальным исчислением, предмет которого есть исчисление производных функций. Первые следы Исчисление конечных разностей конечных разностей видны в некоторых приемах Фермата, Баррова и Лейбница, но основателем способа, как самостоятельного исчисления, следует считать Тейлора. Позднейшими за тем исследователями были Николь, Кондорсе, Эмерсон, Эйлер, Лагранж и Лаплас. Они усовершенствовали эту важную отрасль чистого анализа и показали различные ее приложения к интерполированию и суммированию рядов, к теории соединений и в особенности к теории вероятностей.
|