|
Иллюстрация к статье на тему "Асимптота". Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
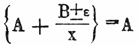
Асимптота - (от греч. слов: α, συν, πίπτω) - несовпадающая. Под асимптотой подразумевается такая линия, которая, будучи неопределенно продолжена, приближается к данной кривой линии или к некоторой ее части так, что расстояние между обеими линиями делается менее всякой данной величины; иначе говоря, Асимптота касается данной кривой линии на бесконечном расстоянии от начала координат. Всякая другая линия, параллельная Асимптота, хотя и приближается непрестанно к кривой, однако, не может быть названа в свою очередь Асимптота, так как расстояние ее от кривой не может быть уменьшено по произволению. Таким образом, число Асимптота для каждой кривой вполне ограничено. С тех пор как греческие геометры стали исследовать свойство кривых линий, образующихся на поверхности конуса от пересечения его плоскостью, стало известным, что ветви гиперболы, будучи неопределенно продолжены, непрестанно сближаются с двумя прямыми линиями, исходящими из центра гиперболы и одинаково наклоненными к ее оси. Эти прямые, о которых упоминает уже Архимед, были еще в древности названы Асимптота и сохранили свое название и по настоящее время. Впоследствии Ньютон показал, что существуют криволинейные Асимптота не только в кривых трансцендентных, но даже в алгебраических, начиная с 3 порядка последних. Действительно, ныне различают Асимптота прямолинейные и криволинейные; но обыкновенно прямолинейной Асимптота присваивают название Асимп., называя криволинейную - асимптотическою кривою. Основываясь на вышеприведенном определении, что прямолинейная Асимптота есть касательная к кривой в точке, бесконечно удаленной от начала координат, легко найти уравнение Асимптота данной кривой. В самом деле, пусть y = f(x) есть уравнение кривой линии; уравнение касательной ее в точке, определенной координатами х и у, будет, как известно, У- у = dy/dx(Х - х) или Y = (dy/dx)Х + у - x(dy/dx). Чтобы перейти от касательной к Асимптота, стоит сделать одно из следующих предположений: 1) x и y = +∞, 2) х = +∞, а у = конечному числу и 3) у = +∞, а х = конечному числу, так как этими предположениями мы выражаем, что точка касания находится на бесконечном расстоянии от начала координат. Так, для гиперболы, определяемой уравнением (x² /a²) - (y²/b²) = 1 н аходим Y = +(b/a)∙[x/√(x ² - a²)]∙X + [ab/√(x² - a²)]. П олагая х = ∞, найдем +(b/a) - [x//√(x² - a²)] = +(b/a)∙[1/√(1 - a²/ x²)] = +(b/a), и +[ab//√(x² - a²)] = 0; с ледовательно, уравнение Асимптота рассматриваемой гиперболы будет У = +(b/a)Х или, что все равно, Y = +(b/a)X и Y = -(b/a)X; последние два уравнения показывают, что гипербола имеет две Асимптота Можно также определить Асимптота следующим образом. Пусть будет У Асимптота = Х + В уравнение Асимптота, не параллельной оси у. Ордината у кривой, соответствующая абсциссе x, для весьма больших величин сей абсциссы будет очень мало разниться от ординаты У а-ты, так что можно ее принять у = Ах + В + ε, подразумевая под ε количество, уничтожающееся вместе с 1/x. Итак, полагая x = ∞, найдем пред. (Y/X) = пред.
|